[CUDA] 準モンテカルロ・シミュレーション Monte Carlo Single Asian Option (with PRNG)

Monte Carlo Single Asian Option (with PRNG) が CUDA C Code Samplesに含まれていましたので実行してみました。

内容はCUDA で、準モンテカルロ法でオプション決定価格を求める実装例です。

===
■参考文献をどうぞ

[amazon_enhanced asin=”4254275064″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4339060232″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4000068520″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4627004796″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]

オプションの価格設定は、金融に遭遇する非常に重要な問題で、1973年に組織化オプション取引の出現以来、金融工学で使われています。より多くの計算が有しているので
オプション価格の効率的な実装を見つけたり、金融関連の問題に適用され、
近代的なアーキテクチャ上でのモデルがより重要になっています。

===

■まず動作結果

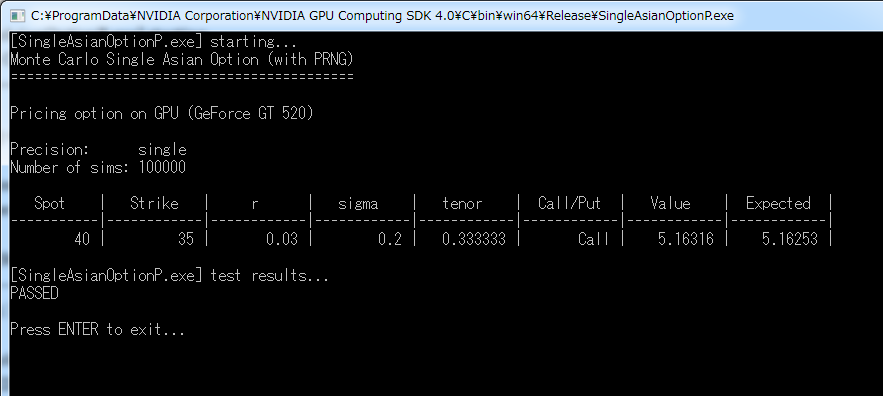
図のものをテキストにしたのは次のとおり。

[SingleAsianOptionP.exe] starting…
Monte Carlo Single Asian Option (with PRNG)
===========================================

Pricing option on GPU (GeForce GT 520)

Precision: single
Number of sims: 100000

Spot | Strike | r | sigma | tenor | Call/Put | Value | Expected |
———–|————|————|————|————|————|————|————|
40 | 35 | 0.03 | 0.2 | 0.333333 | Call | 5.16316 | 5.16253 |

[SingleAsianOptionP.exe] test results…
PASSED

Press ENTER to exit…

■解説

100,000 回シミュレーションを行うバイナリアプリで得られた結果ですが、

そもそもモンテカルロ法はどのように成立したのかを簡単に紹介します。また前述までの内容はモンテカルロ法ではなく準モンテカルロ法である違いについても紹介します。

■モンテカルロ法　（Wikipedia より）

計算理論の分野において、モンテカルロ法とは多項式時間で処理が終了されることは保証されるが、導かれる答えが必ずしも正しいとは限らない乱択アルゴリズム（ランダム・アルゴリズム）と一般に定義される^[1]。一例として素数判定問題におけるミラー-ラビン素数判定法がある。このアルゴリズムは与えられた数値が素数の場合は確実に Yes と答えるが、合成数の場合は非常に少ない確率ではあるが No と答えるべきところを Yes と答える場合がある。

なお、これとは対照的に理論上処理の終了時間が必ずしも多項式時間で終了するとは限らないが、もし答えが得られれば必ず正しい乱択アルゴリズムをラスベガス法と呼ぶ。

計算複雑性理論では、確率的チューリング機械によるモデル化によってモンテカルロ法を用いて解決できる問題のクラスをいくつか定義している。代表的なところでは RPやBPP、PP などがある。これらのクラスと Pや NP との関連性を解明していくことによって、モンテカルロ法のようにランダム性を含むアルゴリズムによって解ける問題の範囲が拡大しているのか（P≠BPP なのか）、それとも単に決定的アルゴリズムで解ける問題の多項式時間の次数を減らしているだけなのか（P=BPP なのか）は計算複雑性理論における主要課題の1つである。現在、NP ⊂ PP 、RP ⊆ NPであることは解っているが BPP と NPとの関係は解っていない。

■準モンテカルロ法　（Wikipedia より）

乱数ではなく、一様分布列 (Low-discrepancy sequence) を使用する方法を準モンテカルロ法 (Quasi-Monte Carlo method) という。乱数を利用するよりも収束が早くなる場合がある。ただし、純粋にランダムな方法ではないので、正解を得られる可能性が確率論的に低下する場合がある。

＝＝＝

■ NVIDIA　はどうしてこれをサンプルアプリにしたのか？

ワタシが思うに、モンテカルロ法の計算式においてオプションの数お計算パスの数との計算時間は計算を最適化することも可能であり、また計算パスがある一定にまで増加されてもパスあたりの計算時間は変化しない GPU 計算の利点を説明するためであると認識しています。

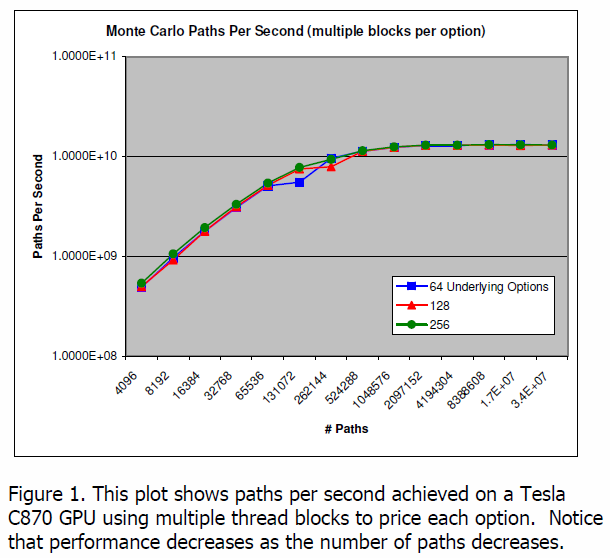
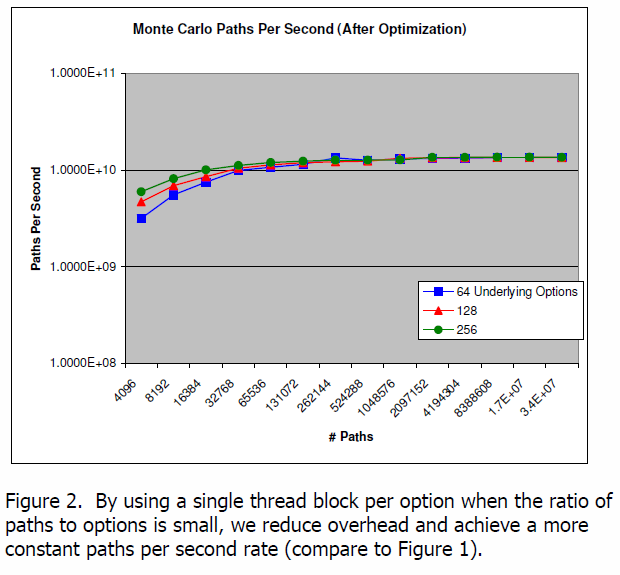
ここでの図式は NVIDIA から無償提供されている「Microsoft Word – MonteCarlo.doc」から引用しました。

以上

＝＝＝

■参考文献をどうぞ

[amazon_enhanced asin=”4254275064″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4339060232″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4000068520″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]　　[amazon_enhanced asin=”4627004796″ container=”” container_class=”” price=”All” background_color=”FFFFFF” link_color=”000000″ text_color=”0000FF” /]